顶点和法线的区别
在齐次坐标系中,一个顶点的表达式为(x, y, z, 1);而一个法线的表达式为(x, y, z, 0)。法线向量的最后一个元素w=0,表示该点位于无穷远处,即只具备方向的唯一性,而不具备位置特性。而顶点位置向量的w=1,这是一个3D的点在齐次坐标系中默认的投影面。顶点位置向量同时具备方向和位置特性。
3✖️3矩阵表达的都是线性变换,无法表达平移变换。为了可以支持矩阵对平移的表达,进而完成平移、缩放和旋转等变换的联合操作(矩阵相乘),通常都用4✖️4矩阵来表达各种变换。对于平移变换,顶点位置和顶点法线向量分别通过4✖️4矩阵变换,可以得到正常的结果。
顶点位置在经过某些矩阵变换之后,对应的顶点法线该如何变换呢?先看一张图:
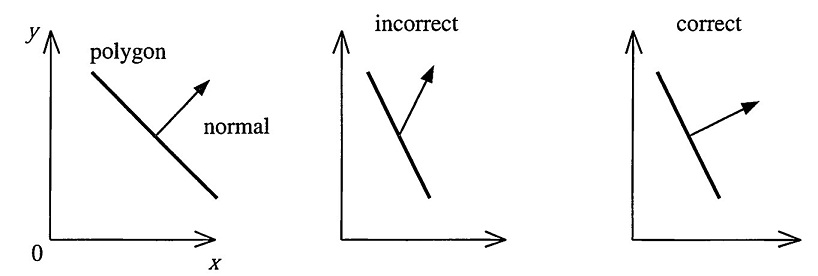
上图是对一个多边形以及一条边上的法线进行缩放变换:X轴上缩放为原来的0.5倍。左边是变换前的状态,中间是将同样的模型变换矩阵应用在法线上的结果,显然是错的,法线并不垂直于切线。最右边的图是正确的结果。如何正确转换呢?法线变换推导
假设某个模型的某个顶点的法线是N,切线是T,用矩阵表达他们乘法是 :
TTN = 0;(矩阵T转置之后才能和N相乘,T转置之后由行向量变为列向量)
假设切线和法线的变换矩阵分别是M和G,则:
(MT)TGN = 0;继而 TTMT GN = 0;既然TTN = 0,则可以推出:
MTG = 0;则法线的转换矩阵为:G = (MT)-1 = (M-1)T。
结论:应用于法线向量的变换矩阵是顶点变换矩阵的逆转置矩阵。法线变换的优化
传统求解逆转置矩阵的方法固然有效,但是求逆矩阵有时候不是必须的,而且有的时候逆矩阵也不存在。逆矩阵是矩阵的伴随矩阵除以矩阵的行列式的值,但是当矩阵是奇异阵的时候,行列式的值是0,这个时候逆矩阵就不存在。
即便是求解一个4*4矩阵的伴随矩阵也是复杂的,而且有时候也不是必须的。由于平移操作不影响法线向量。而且大多数模型变换都是仿射变换。
关于仿射变换(AffineTransform):
AffineTransform类描述了一种二维仿射变换流程图射变换的功能,它是一种二维坐标到二维坐标之间的线性变换,保持二维图形的“平直性”(译注: straightness,即变换后直线还是直线不会打弯,圆弧还是圆弧)和“平行性”(译注:par 常用的仿射变换:旋转、倾斜、平移、缩放allelness,其实是指保二维图形间的相对位置关系不变,平行线还是平行线,而直线上点的位置顺序不变,另特别注意向量间夹角可能会发生变化。仿射变换可以通过一系列的原子变换的复合来实现,包括:平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和错切(Shear)。
因此,他们不会改变齐次坐标的w分量。例如,没有投影变换的时候。因此,这个时候只需要计算矩阵左上方3*3子矩阵的伴随矩阵即可。
在很多情况下,甚至是求解上述的3*3伴随矩阵都不需要。假设我们知道变换矩阵是由一系列平移、旋转、等方缩放(uniform scaling)组成的,平移不影响法线,等比缩放的只影响法线的长度。剩下需要考虑的就只有旋转变换了。而旋转矩阵有一个很重要的特定就是它的转置矩阵和逆矩阵相等。因此,这个时候逆转置矩阵就是原来的矩阵,这个时候就不需要任何计算。
最后需要注意的是,对法线向量进行归一化不总是必须的。如果只有平移和旋转矩阵,那么法线长度不会发生改变。如果也有等方缩放,那么直接用它的缩放因子进行归一化。
针对那些在变换之后,依据三角形边的叉积计算法线的情况,就不需要计算法线变换矩阵了。注意:切向量和法线不同,切线是依据原始的矩阵进行变换的。